−Table of Contents

Datenbanksysteme I

Allgemein

Probleme

Fehlende Datenunabhängigkeit (änderung des Dateiformats)
Redundanz (u.a. Änderungsanomalien)
Schnittstellen (Jeder kocht sein eigenes Süppchen)
Mehrbenutzer System
Datenverlust bei Systemabsturz/deffekt
Zugriffkontrolle

Aufbau

DB-Anwendung
DBS
- DBMS
- DB

Anwendungen (mehrere)
Externe Ebene	Views (mehrere)
	↓↓ Logische Datenunabhängigkeit ↓↓
Konzeptionelle Ebene
	↓↓ Physische Datenunabhängigkeit ↓↓
Interne Ebene	Speicherformat

Anforderungen

Integration einheitlicher Zugriff auf alle Daten einer Anwendung
Operationen auf den Daten (ändern, löschen, …)
Data Dictionary Schema anschauen
Benutzersicheten views
Konsistenzüberwachung bei Änderung
Zugriffskontrolle
Transaktionen
Synchronisation (Mehrbenutzersystem)

Sprachen

Data Definition Language
Data Manipulation Language

Datenmodelleigenschaften

Objekte der Datenbank
Beziehungen zwischen verschiedenen Objekten
Integritätsbedingugen
Angebotenen Operationen (zum Abfragen)

Datenmodelle

Hierarchisches ~
Netzwerk ~ (Art linked list, was den parent im link Ring beinhaltet)
Relationales ~
Objektorientiertes ~
Objekt-Relationales ~

Verbindung zur Datenbank

Optimierung

Scanner/Parser/View-Erzeuger
\| Anfrage (deklarativ) ↓
\| algebraischer Ausdruck ↓
Anfrageoptimierung
\| Auswertungsplan (prozedural) ↓
Ausführung

Kanonischer Auswertungsplan

Query in Funktionsbaum übersetzten

Kaskadierter Kartesische Produkte (nur 2 Eingänge)
Jede WHERE Bedingung einzeln

Beispiel

SELECT A1, A2
FROM R1, R2, R3
WHERE B1, B2

Ergibt $\pi_{A_1, A_2}(\sigma_{B_1}(\sigma_{B_2}(R_1 \times (R_2 \times R_3))))$

Optimierung: Filter so früh wie möglich

Wo kann optimiert werden

Logische Anfrageoptimierung
Auswertungsplan umbauen
Physische Anfrageoptimierung
- Join Strategie
  - Nested Loop
    Kartesisches Produkt Filtern
  - Sort Merge
    Vorher Sortieren, dann mergen
  - Indexed Loop
    Tabelle 1 abarbeiten, Tabelle 2 über Index mergen
- Index Verwenden?

Wie kann optimiert werden

Regelbasiert
Heuristiken
Kostenbasiert
Iterativ Heuristiken ausprobieren und Kostenentwicklung beobachten

Transaktionen

Atomicity
Consistency
Isolation
Durability

Datensicherheit

Technische Fehler

Wann	Was	Undo	Redo
Transaktionsfehler	Rücksetzen	Lokales Undo nicht abgeschlossene Transaktion rückgängig
Systemfehler	Warmstart	Globales Undo nicht abgeschlossene Transaktionen rückgängig	Globales Redo Alle abgeschlossenen Transaktionen nachholen
Medienfehler	Kaltstart	Backup einspielen	Globales Redo Alle abgeschlossenen Transaktionen nachholen

Integrität

Statische Integrität
Einschränkung der Datenbankzustände
Dynamische Integrität
Einschränkung der Zustandsübergänge
Modellinhärente Integrität
- Typintegrität
- Schlüsselintegrität
- Referentielle Integrität

Synchronisation

Anomalien

Lost update

t1	r(x)		w(x)
t2		w(x)

Dirty read/write

t1	w(x)		w(x)
t2		r(x)

Non-repeatable read

t1	r(x)		r(x)
t2		w(x)

Phantom-Problem

Non-repeatable read mit Aggregiertem read

Serialisierung

allgemeiner Schedule	Durcheinander	<latex> $\frac{(m_1 + m_2 + \dots){\color{red}!}}{m_1{\color{red}!} \cdot m_2{\color{red}!} \cdot \dots}$ </latex>
serialisierbarer (allgemeiner) Schedule	Durcheinander kann in Blockform gebracht werden
serieller Schedule	Blockform	<latex> $n{\color{red}!}$ </latex>

Graph Zeichen

Knoten: Transaktionen
Kanten: Abhängigkeiten

Übergang	Markierung
$w_i(x) \rightarrow r_j(x)$	wr(x)
$r_i(x) \rightarrow w_j(x)$	rw(x)
$w_i(x) \rightarrow w_j(x)$	ww(x)

Kein rr(x)

Zyklenfrei? ⇒ Serialisierbar durch topologisches sorieren

Technicken

Pessimistische Ablaufsteuerung (Locking)
Optimistische Ablaufsteuerung (Zeitstempelverfahren)
Notfalls rollback

Anwendung

"MVC" Aufteilungen

	Thin client	Fat client	Stored procedure	Web Application	Application Server
Client	GUI	GUI Logik	GUI Hauptprogramm	Browser	GUI
Application Server					Logik
DB-Server	Logik DB-Schnittstelle DB	DB-Schnittstelle DB	Prozeduren DB-Schnittstelle DB	Webserver Logik DB-Schnittstelle DB	DB-Schnittstelle DB

Interaktion

Call-Level-Schnittstelle (library)
Embedded SQL

Cursor

Declaration
SQL eingeben
Open
Ausführen
Fetch loop
Close

Vorübersetzes SQL mit Platzhaltern

Mathe

Funktionale Abhängigkeiten

Arten

Partielle funktionale Abhängigkeit: $X \rightarrow Y$
Volle funktionale Abhängigkeit: $X \dot{\rightarrow} Y$ (Minimalität)

Axiome

Reflexivität	${\color{ForestGreen}Y} \subseteq {\color{red}X}$	$\Longrightarrow$	${\color{red}X} \rightarrow {\color{ForestGreen}Y}$
Verstärkung	${\color{red}X} \rightarrow {\color{ForestGreen}Y}$	$\Longrightarrow$	${\color{red}X}{\color{RoyalBlue}Z} \rightarrow {\color{ForestGreen}Y}{\color{RoyalBlue}Z}$
Transistivität	${\color{red}X} \rightarrow {\color{ForestGreen}Y} \wedge {\color{ForestGreen}Y} \rightarrow {\color{RoyalBlue}Z}$	$\Longrightarrow$	${\color{red}X} \rightarrow {\color{RoyalBlue}Z}$
Vereinigung	${\color{red}X} \rightarrow {\color{ForestGreen}Y} \wedge {\color{red}X} \rightarrow {\color{RoyalBlue}Z}$	$\Longrightarrow$	${\color{red}X} \rightarrow {\color{ForestGreen}Y}{\color{RoyalBlue}Z}$
Dekomposition	${\color{red}X} \rightarrow {\color{ForestGreen}Y}{\color{RoyalBlue}Z}$	$\Longrightarrow$	${\color{red}X} \rightarrow {\color{ForestGreen}Y} \wedge {\color{red}X} \rightarrow {\color{RoyalBlue}Z}$
Pseudotransitivität	${\color{red}X} \rightarrow {\color{ForestGreen}Y} \wedge {\color{RoyalBlue}Z}{\color{ForestGreen}Y} \rightarrow V$	$\Longrightarrow$	${\color{red}X}{\color{RoyalBlue}Z} \rightarrow V$

Attributhülle

AttrHülle(F,X) mit
F = FDs
X = Start Attributmenge

Starte mit X und wende so lange F ab, bis nichts mehr geht. (“Schau wie weit du kommst”)

Normalisierung

Anomalien

Update~
Nicht alles wird geupdatet
Insert~
Inkonsistentes insert
Delete~
Löschen der letzten Verwendung, löscht auch Objekt

1. NF

Bedingung

Alle Attribute atomar

Attributwerte dürfen nicht …

Listen sein: {Telefon1, Telefon2, Telefon3, …}
Zusammengesetzt sein: (Hausnummer, PLZ, …)

2. NF

Bedingung

Jedes Attribut entweder
voll funktional Abhängig von jedem Schlüsselkandidaten
– oder –
prim (teil eines Schlüsselkandidaten)

Trivial: nur ein einelementiger Schlüsselkandidat ⇒ 2. NF

Sonst: Vom Schlüssel nicht voll funktional Abhängige Attribute werden herausgelöst, in eigene Tabelle

3. NF

Bedingung

Jede FD $X \rightarrow Y$ ist mindestens eins:

tivial
X enthält Schlüsselkandidat
$\forall a \in (Y-X)$ ist prim

Keine (nicht trivialen) FDs unter Nicht-Schlüssel-Attributen

Kanonische Überdeckung
1. Linksreduktion
  Komme ich von X-x und identischem FD dennoch auf Y, dann streiche x aus X
2. Rechtsreduktion
  Komme ich von X und FD ohne y dennoch auf y in Y, dann streiche y aus Y
3. $X \rightarrow \emptyset$ entfernen
4. Gleiche X zusammenfassen
Relationsschema erzeugen und FDs zuweisen
1. Aus jedem FD erzeuge eine Relation mit X als Primärschlüssel und Y als Attribute
2. Ordne jedes FD den Relationen zu, die alle seine “Buchstaben” enthält
Schlüsselkandidat rekonstruieren
Stelle sicher, dass eine Relation einen ehemaligen Schlüsselkandidaten enthält, notfalls erzeuge eine neue mit leerem ohne zugeordnete FDs
Überflüssige Relationen eliminieren
Lösche Relationen, die Teilmenge einer anderen sind.

Boyce-Codee-Normalform

Bedingung

Jede FD $X \rightarrow Y$ ist mindestens eins:

tivial
X enthält Schlüsselkandidat

Keine (nicht trivialen) FDs unter Schlüssel-Attributen

4. NF

Wirkung

Nicht mehrere Tabellen in einer.

Bedingung

Jede MVD $X \twoheadrightarrow Y$ ist mindestens eins:

tivial
X enthält Schlüsselkandidat

MVD (Multi Valued Dependency): Mehre Attributwerte, eines Attributs, sind von der linken Seite abhängig.

Begriffe

Domain
- = Typ
- Kann auch Liste Sein
- endlich
- unendlich (nicht in DB Darstellbar)
- z.B. Int, Sting, Date, {rot, gel, käsekuchen}
Relation = Ausprägung eines Relationsschemata = Menge = {}
Tupel = Zeile = Ausprägung einer Relation = ()
Grad = Stelligkeit = Elemente im Tupel
Relationsschema: Über eine Tabelle
DB-Schema: Über alle Tabellen

Schlüssel

Eigenschaften

Eindeutig
$t_1 \ne t_2 \Rightarrow \pi_S(t_1) \ne \pi_S(t_1)$
Unterschiedliche Tupel ⇒ Unterschiedliche Schlüssel
Minimal
$\text{Eindeutig}(T) \wedge T \subseteq S \Rightarrow T = S$
Keine Teilmenge des Schlüssels erfüllt die 1. Eigenschaft

(Minimal bedeutet nicht: Die wenigsten Attribute)

Schlüssel und FD sind semantische Eigenschaften (nicht anhand von aktueller Ausprägung erkennbar)

Arten

Superschlüssel: Nur 1. Eigenschaft erfüllt ( $S \rightarrow R$ )
Schlüsselkandidat: 1. und 2. Eigenschaft erfüllt ( $S \dot{\rightarrow} R$ )
Primärschlüssel: Ein beliebiger aber fester Schlüsselkandidat

Primes Attribut: Teil eines Schlüsselkandidaten

Beweis

Beispiel: Beweise das S = (A, B) Schlüsselkandidat ist.

Eindeutigkeit
$S \rightarrow R$ herleiten
Minimalität
Zeigen das weder $A \rightarrow R$ noch $B \rightarrow R$ gild

Relationsschemata

geordnet

Schema	R = (id:Integer, Name:String)
Ausprägung	r = {(1, Alice), (2, Bob), (42, Eve)}

ungeordnet (mit Domänenabbildung)

Schema	R = {id, Name} mit dom(id) = Integer, dom(Name) = String
Ausprägung	r = {t1, t2, t3} mit t1(id) = 1, t1(Name) = Alice, t2(id) = 2, t2(Name) = Bob, t3(id) = 42, t3(Name) = Eve

Relationale Algebra

Formel	Name	Iden- tisch	Duplikat- elimi- nation	SQL	Kommentar
$A \cup B$	Vereinigung	X	X	`UNION` `UNION ALL`	Duplikatelimination in SQL nur bei `UNION`
$A - B$	Differenz	X		`EXCEPT` `MINUS`
$A \times B$	Kreuzprodukt Kartesisches Produkt
$\sigma_F(A)$	Selektion			`WHERE`
$\pi_{a, b, \dots}(A)$	Projektion		X	`SELECT`
$A \cap B$	Durchschnitt	X		`INTERSECT`
$A \div B$	Quotient				Allquantor. Die Tupel aus A, die alle Attribute aus jedem B Tupel gleich haben, ohne die B Attribute.
$A \bowtie B$	Natural Join			`NATURAL JOIN t`	Inner-Join (Tupel ohne Partner gehen verloren) Vergleich aller gleichbenannten
$A \underset{a = b}{\bowtie} B$	Equi Join		X	`JOIN t USING(id)`	Inner-Join (Tupel ohne Partner gehen verloren)
$A \underset{a \Theta b}{\bowtie} B$	Theta Join			`JOIN t ON f`	Inner-Join (Tupel ohne Partner gehen verloren) Θ = Vergleichsoperator

Identisch

Relationale Algebra: Typ und Name jedes Attributs muss übereinstimmen (Schemata identisch)
SQL: Typ jedes Attributs muss kompatibel sein (nur die Position ist maßgebend)

Relationale Algebra und SQL

Für jeden relationalen Ausdruck existiert ein SQL statement (SQL ist relational vollständig)
SQL Projektion entfernt nicht immer Duplikate implizit (Explizites DISTINCT bei umsetzung!!)
SQL kann mehr: Sortieren, Aggregation

Relationen-Kalkül

t ∈ Schema ⇔ Schema(t) t[A] ⇔ t.A

Ψ(r | t): Ersetze t in Ψ(r | t) mit dem konkreten Tupel r

Relationale algebra
prozedual (wie)
Relationen-Kalkül
deklarativ (was)
- Tupelkalkül: Variable = ein Tupel
- Bereichskalkül: Variable = einfacher Typ

Quantoren sind nur im Relationenkalkül möglich.

Variable ist …

frei: keinem ∃ oder ∀ zugeordnet
gebunden: einem ∃ oder ∀ zugeordnet
Zuordnungszustand kann sich ändern

Es ist möglich unendlich (nicht speicherbare) Relationen zu beschreiben.
Eine Relation ist sicher wenn alle Vaiablen x einer (gespeicherten) Relation angehören Schema(x).

Tupelkalkül	Bereichskalkül
Alle Großstädte in Bayern
Schema(t) = Schema(Städte) {t \| Städte(t) ∧ f[Land] = Bayern ∧ t[SEinw] ≥ 500000}
In welchem Land liegt Passau
Schema(t) = (Land:String) {t \| (∃ u ∈ Städte)(u.Sname = Passau ∧ u.Land = t.Land}	$\{ x_3 \mid \exists x_1, x_2 : (\text{Städte}(x_1, x_2, x_3) \wedge x_1 = \text{Passau}) \}$
	$\{ x_3 \mid \exists x_2 : (\text{Städte}(\text{Passau}, x_2, x_3)) \}$
CDU-regierte Städte
Schema(t) = Schema(Städte) {t \| Städte(t) ∧ (∃ u ∈ Länder)(u.Lname = t.Land ∧ u.Partei = CDU) }	$\{x_1 \mid \exists x_2, x_3, y_2 : (\text{Städte}(x_1, x_2, x_3) \wedge \text{Länder}(x_3, y_2, \text{CDU}))\}$
SPD alleinregierte Länder
Schema(t) = SChema(Länder) {t \| Länder(t) ∧ (∀ u ∈ Länder)(u.LName = t.LName ⇒ u.Partei = SPD}	$\{x_1 \mid \exists x_2 : (\text{Länder}(x_1, x_2, \text{SPD}) \wedge \neg \exists y_3 : \text{Länder}(x_1, x_2, y_3) \wedge y_3 \ne \text{SPD} \}$
Schema(t) = SChema(Länder) {t \| Länder(t) ∧ (∀ u ∈ Länder)(u.LName = t.LName ⇒ u.Partei = SPD}

Speicher Stukturen

Jeder zusätzlich Schlüssel wirkt sich negativ auf updates aus.

Datenorganisierende Strukturen
Suchbaumverfahren (B+-Baum)
Raumorganisierende Strukturen
dynamische Hash-Verfahren

Seitenarten (für Daten- und Raumorganisierende Strukturen)

Directoryseiten
Verweis auf Datenseiten
Datenseiten
Die eigentlichen Daten

Schlüsselarten

Primärschlüsselsuche
- B+-Baum
- Lineares Hashing
Sekundärschlüsselsuche
- Invertierte Listen

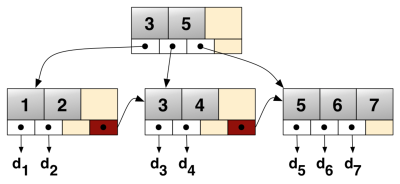
B+ Baum

Alle Daten ausschließlich in den Blättern (Datenseiten)
Schlüssel (Seperatoren) kommen mehrfach in Directoryseiten vor.
Mit rechtem Bruder ausgleichen

Ordnung m
Wurzel: 1 … 2m Kinder
Knoten: m … 2m Kinder

Erweiterbares Hashing (Directory)

Die Zahlen geben an, wie viele Bits “beachtet” werden müssen.
Die Zahl des Diresctorys ist immer größer-gleich der Zahl der Datenseiten, ansonsten Directory Zahl inkrementieren & Directory verdoppeln
Läuft eine Datenseite über ⇒ Split + Zahl inkrementieren

Lineares Hashing (Ohne directory)

$\text{Belegungsfaktor} = \frac{\text{Alle Schlüssel}}{\text{Kapazität in \textit{Primär}seite}} > 0.8 \Rightarrow \text{Expansion}$

Invertierte Listen

Alle Attribute einzeln indizieren
einzeln suchen
Schnittmenge der Ergebnislisten bilden

Reverse pattern matching

Für LIKE “Horst%”

Composite Indizes

mehrere Attribute

Attributwerte werden concatiniert sortiert gespeichert
Reihenfolge wichtig

E/R-Modell

Elemente:

Entitie (eckig)
Relationship (raute)
- Können Attribute haben
Attribute (oval)
- Primärschlüssel unterstreichen
(strich)
- Können Rollen haben
- Pfeil = 1-KArdinalität
- Voller Kringel: 1.. / NOT NULL
- Hohler Kringel: 0.. / NULL
Vererbung (Pyramide)
- Text: “isa”

Umsetzen:

Vererbung
- Eine gemeinsame Tabelle
  – ODER –
- “isa” in einzelne Relationen auflösen
1:1 Relation
1. Beide Relationen zusamenfassen
2. Nur einer der alten Primärschlüssel wird der neue Primärschlüssel

SQL

Typen

`integer`	`integer4`	`int`
`smallint`	`integer2`
`float(`p`)`	`float`		Bits der mantisse (nicht Exponent)
`decimal(`p`,` q`)`	`numeric(`p`,` q`)`		Exakte Komma Zahlen. p Stellen gesamt, davon q Nachkommastellen.
`character(`n`)`	`char(`n`)`
`character varying(`n`)`	`varchar(`n`)`
`date`
`time`
`timestamp`

http://www.postgresql.org/docs/9.2/static/datatype-numeric.html

Constrains

NOT NULL
PRIMARY KEY
UNIQUE
REFERENCES t(a)
DEFAULT w
CHECK f

Integritätsbedingungen

PRIMARY KEY (a1, a2, …)
UNIQUE (a1, a2, …)
FOREIGN KEY (a1, a2, …) REFERENCES t(b1, b2, …)
CHECK f

Schlüssel

Schlüsselkandidat
- UNIQUE
- UNIQUE (a1, a2, …)
Primärschlüssel
- PRIMARY KEY
- PRIMARY KEY (a1, a2, …)
Fremdschlüssel
- REFERENCES t(a)
- FOREIGN KEY (a1, a2, …) REFERENCES t(b1, b2, …)

Fremdschlüssel Zusätze

Folgende sachen können am Ende einer REFERENCES Angabe stehen

ON DELETE SET NULL
Wenn das Referenzierte gelöscht wird, wird dieser auf NULL gesetzt
ON DELETE CASCADE
Wenn das Referenzierte gelöscht wird, wird auch dieser gelöscht
ON UPDATE CASCADE
Wenn das Referenzierte geändert wird, wird auch dieser geändert

Bla

`a + b`	`a - b`	`a * b`	`a / b`
`a = b`	`a <> b`
`a < b`	`a > b`	`a <= b`	`a >= b`
`x BETWEEN a AND b`
`a IS NULL`	`a IS NOT NULL`
`a IN (…)`
`a AND b`	`a OR b`	`a NOT b`

s1 || s2 CHAR_LENGTH(s) SUBSTRING(s FROM pos [FOR len]) a LIKE '...'

% 0…n beliebige Zeichen
_ 1 beliebiges Zeichen

CREATE TABLE name (
  name typ constraints,
  name typ constraints,
  integritätsbedingungen
)

DROP TABLE name

ALTER TABLE name ADD (
  name typ constraints,
  name typ constraints
)

ALTER TABLE name DROP (
  name,
  name
)

ALTER TABLE name MODIFY (
  name typ constraints,
  name typ constraints
)

SELECT [DISTINCT]
  *,
  t.*,
  t.a,
  42,
  32 AS Foo    -- Hier AS
FROM
  t,
  Unisinn u,   -- KEIN AS
  (SELECT ...)
WHERE

INSERT INTO name [(a1, a2)]
VALUES
  (v11, v21),
  (v12, v22)

INSERT INTO name (a1, a2)
(SELECT ...)

UPDATE name
SET
  a1=v1, 
  a2=v2
[WHERE ...]

DELETE FROM name
[WHERE ...]

GRANT
  ALL
  ALL PRIVILEGES
  SELECT
  INSERT
  DELETE
  UPDATE
  UPDATE(a, b)
ON
  t
TO
  TU PUBLIC,
  userName
[WIDTH GRANT OPTION]

REVOKE
  ALL
  ALL PRIVILEGES
  SELECT
  INSERT
  DELETE
  UPDATE
  UPDATE(a, b)
ON
  t
FROM
  TU PUBLIC,
  userName
[RESTRICT | CASCADE]  -- RESTRICT: Nur den user löschen
                      -- CASCADE: nehme die rechte auch denjenigen, die sie vom user bekommen haben

CREATE INDEX name ON t (a1, a2, ...);
DROP INDEX name;

-- Laut script kein START TRANSACTION
SET TRANSACTION READ-ONLY  -- kein INSERT, UPDATE und DELETE. Dafür bessere Transaktionsplanung
SET TRANSACTION READ-WRITE -- default
SAVEPOINT name
COMMIT
ROLLBACK
ROLLBACK TO name

Join

`NATURAL JOIN t`	Natural Join	$A \bowtie B$	Vergleich aller gleichbenannten
`JOIN t USING(id)`	Equi Join	$A \underset{a = b}{\bowtie} B$
`JOIN t ON f`	Theta Join	$A \underset{a \Theta b}{\bowtie} B$	Θ = Vergleichsoperator

inner
outer
- left
- right
- full

Join Art	Verlustfreie Seite		NULL
Join Art	L	R	L	R
`[INNER] JOIN`
`LEFT [OUTER] JOIN`	✓			✓
`RIGHT [OUTER] JOIN`		✓	✓
`FULL [OUTER] JOIN`	✓	✓	✓	✓

Quantoren

WHERE EXISTS (SELECT ...)             -- Ergebnis Form egal
WHERE NOT EXISTS (SELECT ...)         -- Ergebnis Form egal
WHERE ... a Θ ALL (SELECT ...)        -- Ergebnis genau ein Attribut, aber mehre Tupel
WHERE ... a Θ SOME/MANY (SELECT ...)  -- Ergebnis genau ein Attribut, aber mehre Tupel
WHERE ... a IN (SELECT ...)           -- Ergebnis genau ein Attribut, aber mehre Tupel

Grouping

GROUP BY x
HAVING SUM(y) > 42

keine Aggregartfunktionen in WHERE

In SELECT nur erlaubt

Groupierte Attribute
Aggregatfunktionen
- COUNT
- SUM
- AVG
- MAX
- MIN

In SELECT nicht erlaubt

*
An groupierte Elemente gejointe Elemente, die selbst nicht groupiert sind.
Abhilfe:
- Auch nach denen groupieren
- MAX(x)

Befehl	Zähle
Befehl	NULL	doppelte
`COUNT(DISTINCT a)`
`COUNT([ALL] a)`		✓
`COUNT(*)`	✓	✓

Order

ORDER BY a [ASC/DESC], b [ASC/DESC], ...

ASC: 0, 1, 2, … (default)
DESC: 9, 8, 7, …

Mengenoperatoren

Typ jedes Attributs muss kompatibel sein

Nur die Position ist maßgebend
Länge bei Strings egal
Genauigkeit bei Zahlen egal

[Im Gegensatz zur relationalen Algebra, wo Typ und Name jedes Attributs übereinstimmen muss (Schemata identisch)]

$A \cup B$	Vereinigung	`UNION [CORRESPONDING]`	mit Duplikatseliminierung
	Vereinigung	`UNION ALL [CORRESPONDING]`	ohne Duplikatseliminierung
$A - B$	Differenz	`EXCEPT [CORRESPONDING]` `MINUS [CORRESPONDING]`
$A \cap B$	Durchschnitt	`INTERSECT [CORRESPONDING]`

SELECT ...
UNION/UNION ALL/EXCEPT/MINUS/INTERSECT [CORRESPONDING]
SELECT ...

CORRESPONDING beschränkt Ergebniss auf gleiche Namen. Die Position ist dann egal.
Besser: Explizite Auswahl/Sortierung mit SELECT
Tip: Explizites NULL in SELECT bei fehlenden Werten.

View

Nutzen

Übersicht
Datenschutz

Normaler View

CREATE [OR REPLACE] VIEW v AS SELECT ...
DROP VIEW v

Nicht erlaubt in Basisrelation:

ORDER BY

Materialisierter View

INSERT INTO mv (SELECT ...)

Effekt-Konformität

Kein merkbarer unterschied zwischen View und Relation

Teil im View	Angewendete Operation	Problembeschreibung
`SELECT`	`INSERT`	Default (`NULL`) für wegprojezierte Attribute
`SELECT`	`INSER`T `UPDATE` `DELETE`	Nicht möglich, wenn `DISTINCT` oder arithmetische Ausdrücke
`WHERE`	`INSERT` `UPDATE`	Tupel-Migration: Tupel verschwindet, da nicht von `WHERE` erfasst Abhilfe: `WHERE … WITH CHECK OPTION`
`JOIN` `GROUP BY`	`INSERT` `UPDATE` `DELETE`	Nicht möglich
Subquerry	`INSERT` `UPDATE` `DELETE`	Nicht möglich, wenn Selbstbezug

Beispiele

Finde Paare mit gleicher Eigenschaft <code sql> SELECT DISTINCT t1.name, t2.name FROM Foo t1, Foo t2 WHERE

t1.attrib = t2.attrib
AND
t1.name < t2.name  -- Macht aus  (AA, AB, BA, BB) : (AB)